【CSP】CSP-J 2024真题 | 扑克牌 luogu-P11227 （相当于GESP三级左右水平）

CSP-J 2024真题- 扑克牌，模拟考点，适合GESP二、三级左右水平的考生练习（二级需要先了解字符串），难度⭐☆☆☆☆，洛谷难度等级入门。

P11227 [CSP-J 2024] 扑克牌

题目要求

题目描述

小 P 从同学小 Q 那儿借来一副 $n$ 张牌的扑克牌。

本题中我们不考虑大小王，此时每张牌具有两个属性：花色和点数。花色共有 $4$ 种：方片、草花、红桃和黑桃。点数共有 $13$ 种，从小到大分别为 $\tt{A 2 3 4 5 6 7 8 9 T J Q K}$。注意：点数 $10$ 在本题中记为 $\tt T$。

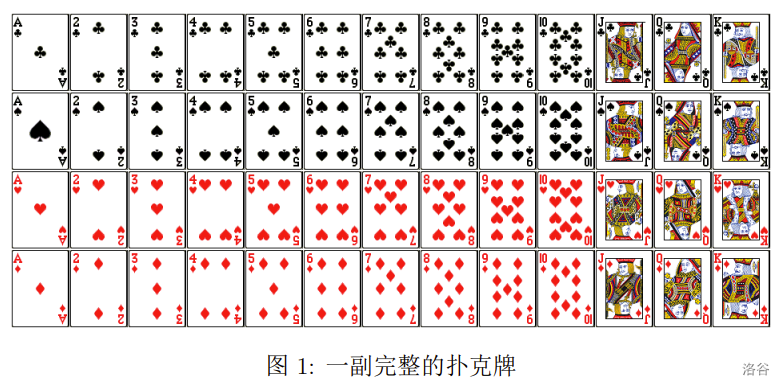
我们称一副扑克牌是完整的，当且仅当对于每一种花色和每一种点数，都恰好有一张牌具有对应的花色和点数。由此，一副完整的扑克牌恰好有 $4 \times 13 = 52$ 张牌。以下图片展示了一副完整的扑克牌里所有的 52 张牌。

小 P 借来的牌可能不是完整的，为此小 P 准备再向同学小 S 借若干张牌。可以认为小 S 每种牌都有无限张，因此小 P 可以任意选择借来的牌。小 P 想知道他至少得向小 S 借多少张牌，才能让从小 S 和小 Q 借来的牌中，可以选出 $52$ 张牌构成一副完整的扑克牌。

为了方便你的输入，我们使用字符 $\tt D$ 代表方片，字符 $\tt C$ 代表草花，字符 $\tt H$ 代表红桃，字符 $\tt S$ 代表黑桃，这样每张牌可以通过一个长度为 $2$ 的字符串表示，其中第一个字符表示这张牌的花色，第二个字符表示这张牌的点数，例如 $\tt{CA}$ 表示草花 $\tt A$，$\tt{ST}$ 表示黑桃 $\tt T$（黑桃 10）。

输入格式

输入的第一行包含一个整数 $n$ 表示牌数。

接下来 $n$ 行：

每行包含一个长度为 $2$ 的字符串描述一张牌，其中第一个字符描述其花色，第二个字符描述其点数。

输出格式

输出一行一个整数，表示最少还需要向小 S 借几张牌才能凑成一副完整的扑克牌。

输入输出样例 #1

输入 #1

1
SA

输出 #1

51

输入输出样例 #2

输入 #2

4
DQ
H3
DQ
DT

输出 #2

49

说明/提示

【样例 1 解释】

这一副牌中包含一张黑桃 $\tt A$，小 P 还需要借除了黑桃 $\tt A$ 以外的 51 张牌以构成一副完整的扑克牌。

【样例 2 解释】

这一副牌中包含两张方片 $\tt Q$、一张方片 $\tt T$（方片 10）以及一张红桃 3，小 P 还需要借除了红桃 3、方片 $\tt T$ 和方片 $\tt Q$ 以外的 $49$ 张牌。

【样例 3 解释】

见选手目录下的 poker/poker3.in 与 poker/poker3.ans。

这一副扑克牌是完整的，故不需要再借任何牌。

该样例满足所有牌按照点数从小到大依次输入，点数相同时按照方片、草花、红桃、黑桃的顺序依次输入。

【数据范围】

对于所有测试数据，保证：$1 \leq n \leq 52$，输入的 $n$ 个字符串每个都代表一张合法的扑克牌，即字符串长度为 $2$，且第一个字符为 $\tt{D C H S}$ 中的某个字符，第二个字符为 $\tt{A 2 3 4 5 6 7 8 9 T J Q K}$ 中的某个字符。

测试点编号	$n \leq$	特殊性质
$1$	$1$	A
$2\sim 4$	$52$	A
$5\sim 7$	$52$	B
$8\sim 10$	$52$	无

特殊性质 A：保证输入的 $n$ 张牌两两不同。

特殊性质 B：保证所有牌按照点数从小到大依次输入，点数相同时按照方片、草花、红桃、黑桃的顺序依次输入。

---

题目分析

本题的核心任务是：计算还需要多少张牌才能凑齐一副 52 张的完整扑克牌。

1. 问题分析

一副完整的扑克牌（不含大小王）共有 52 张。 题目给了我们 $n$ 张牌，但这 $n$ 张牌里可能会有重复的牌（比如小 P 借了两张红桃 A）。 多余的重复牌对“凑齐一副牌”没有帮助，我们只关心有多少种不同的牌。

假设我们手里有 $U$ 张不同的牌 (Unique Cards)。那么还需要借的牌数就是： \(\text{Answer} = 52 - U\)

2. 方法一：利用 STL set (std::set)

这是最简单直接的方法。

• std::set 是 C++ 标准库中的集合容器，它的特性是自动去重。
• 当我们把输入的字符串（牌）插入 set 时，如果集合里已经有这张牌了，它就不会再次插入。
• 最后，set.size() 就是不重复的牌的数量 $U$。

此方法代码简洁，适合无需极致优化、且对 map/set 熟悉的同学。

时间复杂度$O(N \log N)$ 或 $O(N \log U)$

• std::set 的底层实现通常是 红黑树 (Red-Black Tree)，这是一种自平衡二叉搜索树。
• 每次插入操作 (insert) 的时间复杂度是 $O(\log \text{Size})$，其中 $\text{Size}$ 是当前集合中元素的个数。
• 我们要进行 $N$ 次插入操作。在最坏情况下（所有牌都不重复），集合大小会从 0 增长到 $N$。
• 因此总时间复杂度约为 $O(N \log N)$。
• 注：由于扑克牌种类最多只有 52 种（常数），实际上 $\log 52$ 是个常数，所以在大数据量下也可以近似看作 $O(N)$。

3. 方法二：利用布尔数组 (bool array)

如果你不想使用 set 或者 map，我们也可以用数组来模拟“去重”的过程。

映射思想：每一张牌都由“花色”和“点数”唯一确定。我们可以定义一个二维数组 bool has_card[4][14]。

• 第一维表示花色（0:方片, 1:草花, 2:红桃, 3:黑桃）。
• 第二维表示点数（1:A, 2-9, 10:T, 11:J, 12:Q, 13:K）。

步骤：

1. 初始化数组全为 false。
2. 读入每张牌，解析其花色和点数，计算对应的下标。
3. 如果 has_card[suit][rank] 为 false，说明这张牌是第一次见：
   • 标记为 true。
   • 计数器 count 加 1。
4. 如果已经是 true，说明重复了，忽略。
5. 最终输出 52 - count。

这种方法的时间复杂度是 $O(N)$，比 set 更快，且无需额外的数据结构。

---

当然，你直接用字符串数组，每次插入前遍历一下，判断是否已经存在，如果不存在就插入，计数器加一，也是可以的。

这种方法时间复杂度是 $O(N^2)$，比 set 更慢，但对于 $N \leq 52$ 的数据来说，也是可以接受的。

---

示例代码

方法一：利用 std::set 自动去重

#include <iostream>
#include <set>
#include <string>

// P11227 [CSP-J 2024] 扑克牌
// 题目要求计算还需多少张牌才能凑齐一副52张牌（不含大小王）
// 输入 n 张牌，可能有重复，我们需要统计有多少张**不重复**的牌
// std::set 特性：自动去重，非常适合本题

int main() {
    std::ios_base::sync_with_stdio(false);
    std::cin.tie(NULL);

    int n;
    std::cin >> n;

    std::set<std::string> cards;  // 定义一个存储 string 的集合，会自动去重
    for (int i = 0; i < n; i++) {
        std::string card;
        std::cin >> card;
        cards.insert(card);  // 插入元素，如果已存在则不会重复插入
    }

    // std::set 常用操作示例（本题不需要，仅作展示）：
    // if (cards.count("DA")) { ... } // 查找是否存在 "DA"
    // cards.erase("DA"); // 删除 "DA"
    // cout << cards.size(); // 获取元素个数

    // 一副牌总共 52 张，我们手里有 cards.size() 张不同的牌
    // 所以还需要 52 - cards.size() 张
    std::cout << 52 - cards.size() << std::endl;

    return 0;
}

方法二：利用布尔数组 (bool array) - 【推荐】

此方法更加基础，不依赖 STL，适合初学者理解“映射”和“标记”的思想。

#include <iostream>
#include <string>

// P11227 [CSP-J 2024] 扑克牌
// 方法二：利用布尔数组进行标记去重

// 定义一个二维数组用来标记每张牌是否出现过
// 第 1 维表示花色：0:D, 1:C, 2:H, 3:S
// 第 2 维表示点数：1:A, 2-9, 10:T, 11:J, 12:Q, 13:K
bool has_card[4][14]; 

// 辅助函数：将花色字符转换为 0-3 的整数
int get_suit_index(char suit) {
    if (suit == 'D') return 0; // Diamond 方片
    if (suit == 'C') return 1; // Club 草花
    if (suit == 'H') return 2; // Heart 红桃
    if (suit == 'S') return 3; // Spade 黑桃
    return -1; // 为了安全加一个返回值，实际上题目保证输入合法
}

// 辅助函数：将点数字符转换为 1-13 的整数
int get_rank_index(char rank) {
    if (rank >= '2' && rank <= '9') {
        return rank - '0'; // '2'-'9' -> 2-9
    }
    if (rank == 'A') return 1;
    if (rank == 'T') return 10;
    if (rank == 'J') return 11;
    if (rank == 'Q') return 12;
    if (rank == 'K') return 13;
    return -1;
}

int main() {
    // 优化 I/O 效率（对于本题数据量其实不需要，但养成习惯很好）
    std::ios_base::sync_with_stdio(false);
    std::cin.tie(NULL);

    int n;
    std::cin >> n;

    int unique_count = 0; // 记录不重复的牌的数量

    for (int i = 0; i < n; i++) {
        std::string card;
        std::cin >> card;

        char suit_char = card[0];
        char rank_char = card[1];

        int suit_idx = get_suit_index(suit_char);
        int rank_idx = get_rank_index(rank_char);

        // 核心逻辑：检查是否已经出现过
        if (has_card[suit_idx][rank_idx] == false) {
            // 如果没出现过，标记为 true，并增加计数
            has_card[suit_idx][rank_idx] = true;
            unique_count++;
        }
        // 如果 has_card[...][...] 已经是 true，说明这张牌之前借过了，
        // 这一张是多余的，直接忽略，不增加计数。
    }

    // 完整的牌有 52 张，我们需要借的牌数 = 52 - 手里有的唯一牌数
    std::cout << 52 - unique_count << std::endl;

    return 0;
}

---

所有代码已上传至Github：https://github.com/lihongzheshuai/yummy-code

GESP 学习专题站：GESP WIKI

“luogu-”系列题目可在洛谷题库进行在线评测。

“bcqm-”系列题目可在编程启蒙题库进行在线评测。

欢迎加入：Java、C++、Python技术交流QQ群(982860385)，大佬免费带队，有问必答

欢迎加入：C++ GESP/CSP认证学习QQ频道，考试资源总结汇总

欢迎加入：C++ GESP/CSP学习交流QQ群(688906745)，考试认证学员交流，互帮互助

GESP/CSP 认证学习微信公众号