【GESP】C++四级考试大纲知识点梳理, (8) 冒泡、插入、选择排序

发表于 2025/06/29 更新于 2025/06/29

作者 OneCoder

次浏览 22 分钟阅读

GESP C++四级官方考试大纲中，共有11条考点，本文针对第8条考点进行分析介绍。

（8）掌握排序算法中的冒泡排序、插入排序、选择排序的算法思想、排序步骤及代码实现。

四级其他考点回顾：

【GESP】C++四级考试大纲知识点梳理, (1) 指针
【GESP】C++四级考试大纲知识点梳理, (2) 结构体和二维数组
【GESP】C++四级考试大纲知识点梳理, (3) 模块化和函数
【GESP】C++四级考试大纲知识点梳理, (4) 变量和作用域
【GESP】C++四级考试大纲知识点梳理, (5) 值传递
【GESP】C++四级考试大纲知识点梳理, (6) 递推算法
【GESP】C++四级考试大纲知识点梳理, (7) 排序算法基本概念

下面分别介绍三种经典的内排序算法——冒泡排序、插入排序和选择排序的核心思想、具体步骤及其 C++ 代码实现。

一、冒泡排序（Bubble Sort）

冒泡排序（bubble sort）通过连续地比较与交换相邻元素实现排序。这个过程就像气泡从底部升到顶部一样，因此得名冒泡排序。

1.1 算法思想

“相邻两两比较，大的往后冒”

🎯 思想要点：

每轮从前往后扫描，比较相邻元素。
如果前面的数大于后面的，就交换。
一轮结束后，最大值沉到末尾。
重复 n-1 轮，直到全部有序。
可设置“是否发生交换”的标志位，优化提前结束。

1.2 算法流程

外层循环从数组首位开始，控制趟数，共需 n−1 趟（n 为元素个数）。
内层循环在未排序区间内（[0, n−i−1]）依次比较相邻元素，若前者 > 后者，则交换。
重复直到整个序列有序。

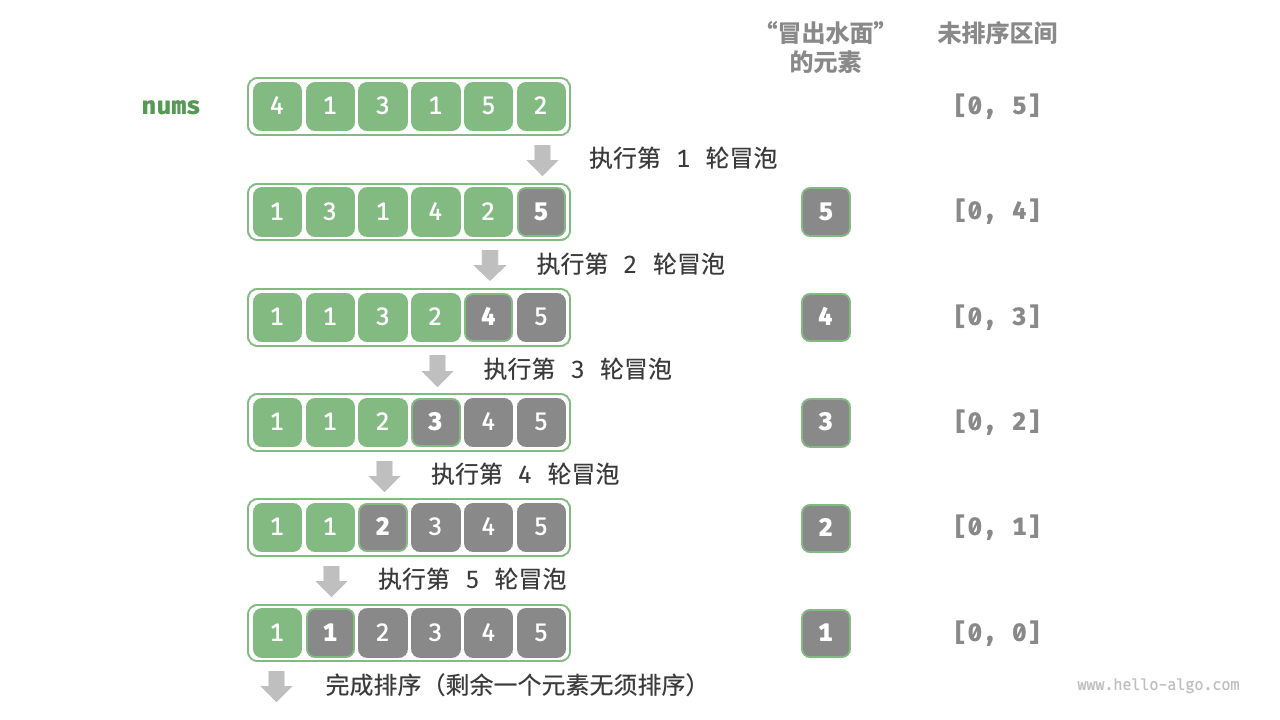
1.2.1 流程示意

图片来自开源书籍：《Hello，算法》

1.3 时间复杂度

最优 $O(n)$，当序列已经有序时，只需一趟即可（可加标志位提前退出）。
平均/最差均为 $O(n^2)$。

1.4 空间复杂度

$O(1)$，仅需要常数个辅助变量（交换时的临时变量）。
属于原地排序算法。

1.5 代码示例

  
#include <iostream>
#include <vector>
using namespace std;

// 冒泡排序函数
void bubbleSort(vector<int>& a) {
    int n = a.size();
    // 外层循环控制排序轮数，n-1轮
    for (int i = 0; i < n - 1; ++i) {
        // 设置标志位，用于优化：如果一轮中没有发生交换，则数组已经有序
        bool swapped = false;
        // 内层循环进行相邻元素比较，每轮将最大值冒泡到末尾
        for (int j = 0; j < n - i - 1; ++j) {
            // 如果前一个元素大于后一个元素，则交换
            if (a[j] > a[j + 1]) {
                swap(a[j], a[j + 1]);
                swapped = true;  // 发生交换，设置标志位
            }
        }
        // 如果没有发生交换，说明数组已经有序，提前退出
        if (!swapped) break;
    }
}

int main() {
    // 测试用例
    vector<int> arr = {4, 1, 3, 1, 5, 2};
    // 调用冒泡排序函数
    bubbleSort(arr);
    // 打印排序后的数组
    for (int num : arr) cout << num << " ";
    return 0;
}

输出结果：

1 1 2 3 4 5

1.5.1 冒泡排序执行过程演示

初始数组：

[4, 1, 3, 1, 5, 2]

第1轮（将最大数“冒”到最后）：

比较 4 和 1 → 交换 → [1, 4, 3, 1, 5, 2]
比较 4 和 3 → 交换 → [1, 3, 4, 1, 5, 2]
比较 4 和 1 → 交换 → [1, 3, 1, 4, 5, 2]
比较 4 和 5 → 无交换
比较 5 和 2 → 交换 → [1, 3, 1, 4, 2, 5]

第2轮（次大数冒到倒数第二）：

比较 1 和 3 → 无交换
比较 3 和 1 → 交换 → [1, 1, 3, 4, 2, 5]
比较 3 和 4 → 无交换
比较 4 和 2 → 交换 → [1, 1, 3, 2, 4, 5]

第3轮：

比较 1 和 1 → 无交换
比较 1 和 3 → 无交换
比较 3 和 2 → 交换 → [1, 1, 2, 3, 4, 5]

第4轮：

比较 1 和 1 → 无交换
比较 1 和 2 → 无交换

第5轮：

比较 1 和 1 → 无交换

✅ 最终结果：[1, 1, 2, 3, 4, 5]

可视化运行：

全屏观看 >

1.6 小结

特性	说明
时间复杂度	最优：$O(n)$ - 数组已经有序平均：$O(n^2)$ 最差：$O(n^2)$ - 数组完全逆序
空间复杂度	$O(1)$ - 只需要常数个临时变量
稳定性	稳定 - 相等元素相对位置不变
原地排序	是 - 不需要额外空间
适用场景	1. 数据规模较小 2. 数据接近有序 3. 需要稳定排序 4. 代码简单易实现
优化方案	1. 添加标志位提前结束 2. 记录最后交换位置 3. 双向冒泡
缺点	1. 大规模数据效率低 2. 交换次数较多

二、插入排序（Insertion Sort）

插入排序（insertion sort）是一种简单的排序算法，它的工作原理与手动整理一副牌的过程非常相似。

2.1 算法思想

“构建有序区，把当前元素插入到前面合适的位置”

🎯 思想要点：

把数组分成 有序区 和 无序区。
初始有序区是第一个元素。
每次从无序区取一个数，从后往前比较插入到有序区。
插入过程中，遇到比当前元素大的，统统右移。

2.2 算法流程

初始时，已排序区间为第 0 个元素。
从索引 1 开始，取出 key = a[i]，在 [0, i-1] 中从后向前扫描，所有大于 key 的元素依次右移一位。
将 key 插入到空出的位置。
重复直至末尾。

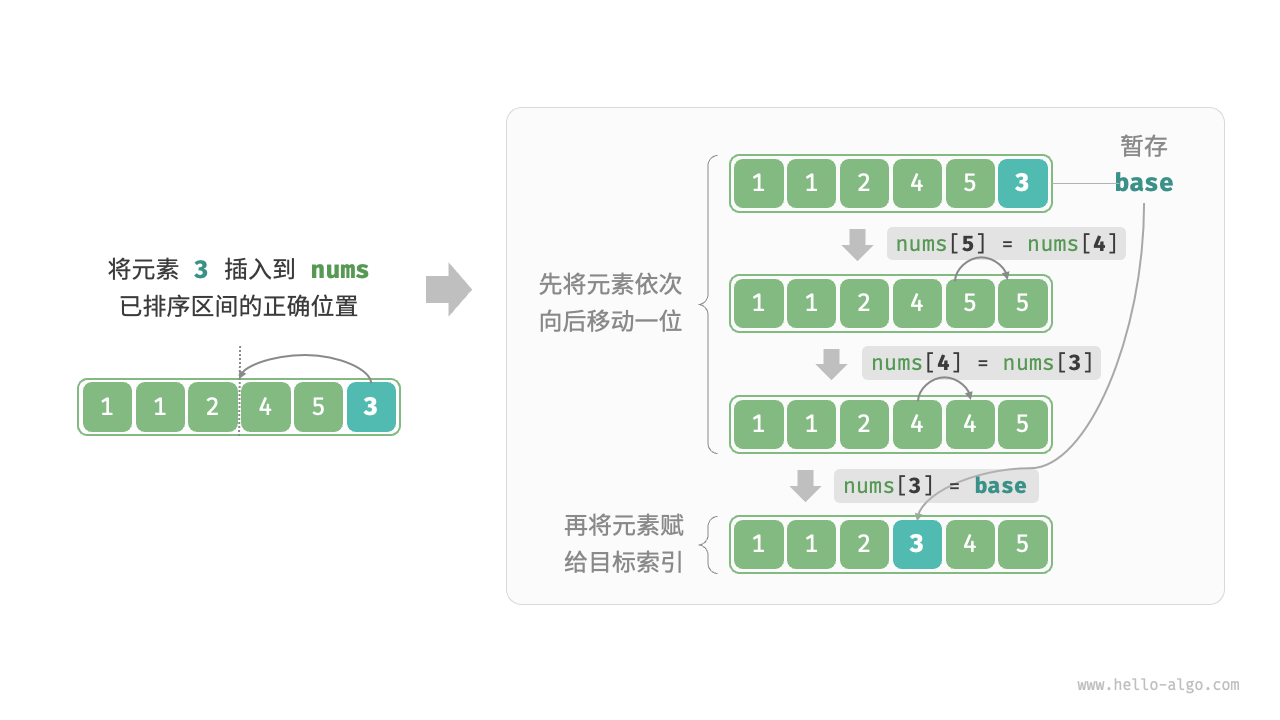
2.2.1 流程示意

图片来自开源书籍：《Hello，算法》

2.3 时间复杂度

最优 $O(n)$，当序列已近乎有序，仅需简单比较。
平均/最差均为 $O(n^2)$。

2.4 空间复杂度

$O(1)$，只需要一个临时变量存储 key 值。
属于原地排序算法。
不需要额外的辅助空间。

2.5 代码示例

  
#include <iostream>
#include <vector>
using namespace std;

// 插入排序函数，参数为待排序的整型向量的引用
void insertionSort(vector<int>& a) {
    // 获取数组长度
    int n = a.size();
    // 从第二个元素开始遍历，因为第一个元素可以视为已排序
    for (int i = 1; i < n; ++i) {
        // 保存当前要插入的元素
        int key = a[i];
        // j指向已排序区间的最后一个元素
        int j = i - 1;
        // 从后向前扫描已排序区间，将所有大于key的元素都向后移动一位
        while (j >= 0 && a[j] > key) {
            // 元素后移
            a[j + 1] = a[j];
            // 继续向前扫描
            --j;
        }
        // 找到key的正确插入位置，将key插入
        a[j + 1] = key;
    }
}

int main() {
    // 创建测试数组
    vector<int> arr = {4, 1, 3, 1, 5, 2};
    // 调用插入排序函数
    insertionSort(arr);
    // 打印排序后的数组
    for (int num : arr) cout << num << " ";
    return 0;
}

输出结果：

1 1 2 3 4 5

2.5.1 插入排序执行过程演示

初始数组：

[4, 1, 3, 1, 5, 2]

第1步：插入 1:

1 < 4，向后移 → [4, 4, 3, 1, 5, 2] → 插入 → [1, 4, 3, 1, 5, 2]

第2步：插入 3:

3 < 4，向后移 → [1, 4, 4, 1, 5, 2]
3 > 1 → 插入 → [1, 3, 4, 1, 5, 2]

第3步：插入 1：

1 < 4 → [1, 3, 4, 4, 5, 2]
1 < 3 → [1, 3, 3, 4, 5, 2]
1 == 1 → 插入 → [1, 1, 3, 4, 5, 2]

第4步：插入 5（无需移动）：

→ [1, 1, 3, 4, 5, 2]

第5步：插入 2：

2 < 5 → [1, 1, 3, 4, 5, 5]
2 < 4 → [1, 1, 3, 4, 4, 5]
2 < 3 → [1, 1, 3, 3, 4, 5]
插入 → [1, 1, 2, 3, 4, 5]

✅ 最终结果：[1, 1, 2, 3, 4, 5]

可视化运行：

全屏观看 >

2.6 小结

特性	说明
时间复杂度	最优：$O(n)$ - 数组已经有序平均：$O(n^2)$ 最差：$O(n^2)$ - 数组完全逆序
空间复杂度	$O(1)$ - 只需要一个临时变量存储 key
稳定性	稳定 - 相等元素相对位置不变
原地排序	是 - 不需要额外空间
适用场景	1. 数据规模较小 2. 数据接近有序 3. 需要稳定排序 4. 代码简单易实现
优化方案	1. 二分查找插入位置 2. 缩小有序区间扫描范围 3. Shell 排序改进
优点	1. 稳定排序 2. 适合小规模数据 3. 对近乎有序数据效率高
缺点	1. 大规模数据效率低 2. 元素移动次数较多

三、选择排序（Selection Sort）

选择排序（selection sort）的工作原理非常简单：开启一个循环，每轮从未排序区间选择最小的元素，将其放到已排序区间的末尾。

3.1 算法思想

“每轮选择最小值，放到最前面”

🎯 思想要点：

将数组分成已排序区和未排序区。
每轮在未排序区中找到最小元素。
与未排序区起始元素交换，扩展已排序区。
不管顺序如何，总是 n-1 轮比较+交换。

⚠️ 注意：

与冒泡不同，它是先“找”再交换，而不是每次都交换。

3.2 算法流程

选择排序的具体执行流程如下:

初始化已排序和未排序区间
- 将数组分成两个区间:已排序区间 [0, i-1] 和未排序区间 [i, n-1]
- 初始时已排序区间为空,未排序区间为整个数组
外层循环遍历未排序区间
- 循环变量 i 从 0 到 n-2
- i 表示当前已排序区间的末尾位置
- 每轮循环会将一个最小值放到已排序区间末尾
内层循环寻找最小值
- 在未排序区间 [i, n-1] 中扫描
- 用变量 minIdx 记录当前找到的最小值的索引
- 初始时 minIdx = i
- 遍历比较每个元素与 minIdx 位置的元素
- 若发现更小的元素则更新 minIdx
交换操作
- 如果找到的最小值索引 minIdx 不等于 i
- 则将 a[i] 与 a[minIdx] 交换位置
- 这样最小值就被放到了已排序区间的末尾
重复执行直到结束
- 重复步骤 2-4,直到整个数组有序
- 总共需要 n-1 轮操作
- 每轮都会将一个最小值放到正确位置

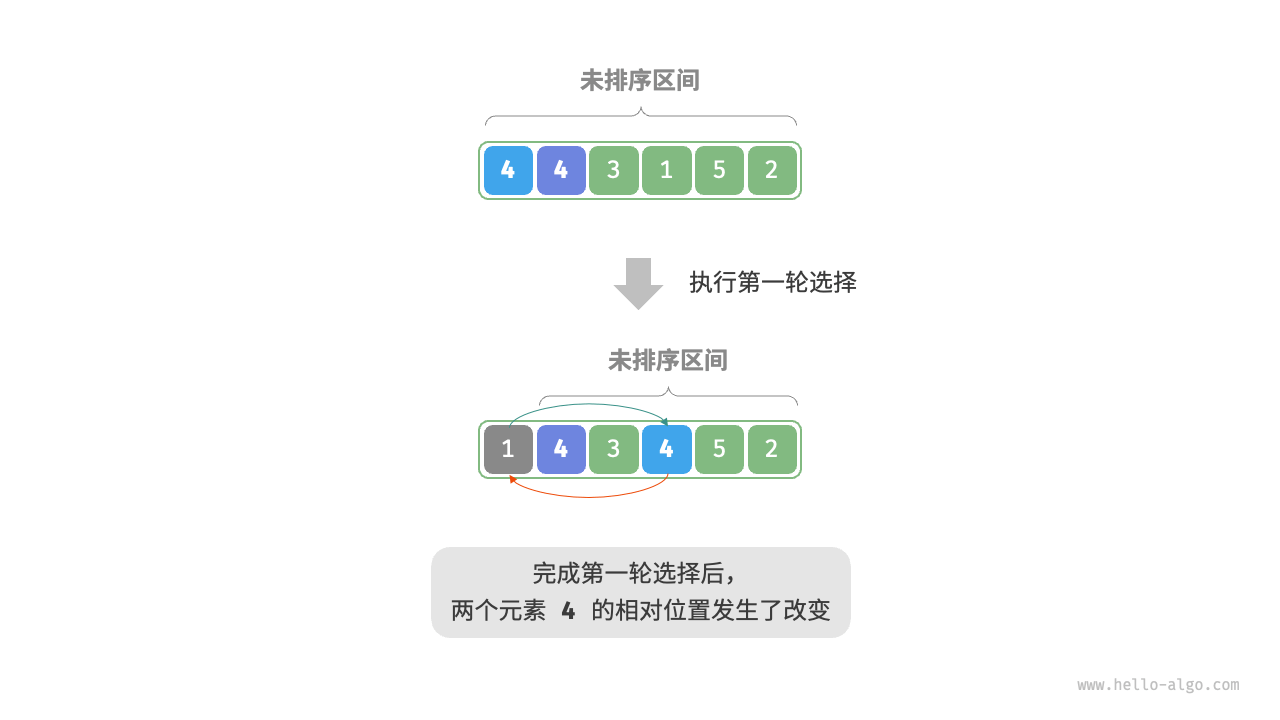
⚠️ 注意：

选择排序是不稳定的，如图所示：
图片来自开源书籍：《Hello，算法》

3.3 时间复杂度

无论初始状态，始终需要 $\frac{n(n-1)}{2}$ 次比较，都是 $O(n^2)$。

3.4 空间复杂度

$O(1)$，只需要一个变量记录最小值索引。
属于原地排序算法。
不需要额外的辅助空间。

3.5 代码示例

  
#include <iostream>
#include <vector>
using namespace std;

// 选择排序函数
void selectionSort(vector<int>& a) {
    int n = a.size();
    // 外层循环，i表示已排序区间的末尾
    for (int i = 0; i < n - 1; ++i) {
        // minIdx记录未排序区间中最小元素的索引
        int minIdx = i;
        // 内层循环在未排序区间[i+1, n-1]中寻找最小元素
        for (int j = i + 1; j < n; ++j) {
            // 如果找到更小的元素，更新minIdx
            if (a[j] < a[minIdx]) {
                minIdx = j;
            }
        }
        // 如果找到的最小元素不是当前位置，则交换
        if (minIdx != i) swap(a[i], a[minIdx]);
    }
}

int main() {
    // 测试用例
    vector<int> arr = {4, 1, 3, 1, 5, 2};
    // 调用选择排序函数
    selectionSort(arr);
    // 打印排序后的数组
    for (int num : arr) cout << num << " ";
    return 0;
}

输出结果：

1 1 2 3 4 5

3.5.1 选择排序流程示意

初始数组：

[4, 1, 3, 1, 5, 2]

第1轮：

选最小（1）与 4 交换 → [1, 4, 3, 1, 5, 2]

第2轮：

选最小（1）与 4 交换 → [1, 1, 3, 4, 5, 2]

第3轮：

选最小（2）与 3 交换 → [1, 1, 2, 4, 5, 3]

第4轮：

选最小（3）与 4 交换 → [1, 1, 2, 3, 5, 4]

第5轮：

选最小（4）与 5 交换 → [1, 1, 2, 3, 4, 5]

✅ 最终结果：[1, 1, 2, 3, 4, 5]

可视化运行：

全屏观看 >

3.6 小结

特性	说明
时间复杂度	最优/平均/最差均为 $O(n^2)$
空间复杂度	$O(1)$ - 只需要一个变量记录最小值索引
稳定性	不稳定 - 可能改变相等元素的相对位置
原地排序	是 - 不需要额外空间
适用场景	1. 数据规模较小 2. 对稳定性要求不高 3. 需要最少的交换次数
优化方案	1. 同时找最大最小值 2. 堆排序改进
优点	1. 交换次数最少 2. 实现简单 3. 不占用额外内存
缺点	1. 时间复杂度固定 2. 不稳定排序 3. 大规模数据效率低

四、三种排序总结对比

特性	冒泡排序	插入排序	选择排序
时间复杂度	最优：$O(n)$ 平均：$O(n^2)$ 最差：$O(n^2)$	最优：$O(n)$ 平均：$O(n^2)$ 最差：$O(n^2)$	最优/平均/最差：$O(n^2)$
空间复杂度	$O(1)$	$O(1)$	$O(1)$
稳定性	稳定	稳定	不稳定
原地排序	是	是	是
优点	1. 实现简单 2. 稳定排序 3. 适合小规模数据	1. 稳定排序 2. 适合小规模数据 3. 对近乎有序数据高效	1. 交换次数最少 2. 实现简单 3. 不占用额外内存
缺点	1. 交换次数多 2. 大规模数据效率低	1. 移动次数多 2. 大规模数据效率低	1. 时间复杂度固定 2. 不稳定排序
适用场景	1. 数据规模较小 2. 数据接近有序 3. 需要稳定排序	1. 数据规模较小 2. 数据接近有序 3. 需要稳定排序	1. 数据规模较小 2. 对稳定性要求不高 3. 需要最少交换次数

三种算法都属于简单直观的内部排序，适合小规模或初学时理解排序思想。对于大规模数据，建议学习快速排序、归并排序、堆排序等更高效的算法。

所有代码已上传至Github：https://github.com/lihongzheshuai/yummy-code
GESP各级别考纲、真题讲解、知识拓展和练习清单等详见【置顶】【GESP】C++ 认证学习资源汇总
“luogu-”系列题目已加入洛谷Java、C++初学团队，作业清单，可在线评测，团队名额有限。
“bcqm-”系列题目可在编程启蒙题库进行在线评测。

欢迎加入：Java、C++、Python技术交流QQ群(982860385)，大佬免费带队，有问必答
欢迎加入：C++ GESP/CSP认证学习QQ频道，考试资源总结汇总
欢迎加入：C++ GESP/CSP学习交流QQ群(688906745)，考试认证学员交流，互帮互助

GESP/CSP 认证学习微信公众号

GESP, 四级

GESP C++

本文由作者按照 CC BY 4.0 进行授权

一、冒泡排序（Bubble Sort）

1.1 算法思想

1.2 算法流程

1.2.1 流程示意

1.3 时间复杂度

1.4 空间复杂度

1.5 代码示例

1.5.1 冒泡排序执行过程演示

1.6 小结

二、插入排序（Insertion Sort）

2.1 算法思想

2.2 算法流程

2.2.1 流程示意

2.3 时间复杂度

2.4 空间复杂度

2.5 代码示例

2.5.1 插入排序执行过程演示

2.6 小结

三、选择排序（Selection Sort）

3.1 算法思想

3.2 算法流程

3.3 时间复杂度

3.4 空间复杂度

3.5 代码示例

3.5.1 选择排序流程示意

3.6 小结

四、三种排序总结对比

热门标签