【GESP】C++四级真题 luogu-B4264 [GESP202503 四级] 二阶矩阵

GESP C++四级2025年3月真题。本题主要考查二维数组的应用。属于四级题中的简单题。难度⭐⭐☆☆☆。本题在洛谷评定为入门。

luogu-B4264 [GESP202503 四级] 二阶矩阵

题目要求

题目描述

小 A 有一个 $n$ 行 $m$ 列的矩阵 $A$。

小 A 认为一个 $2 \times 2$ 的矩阵 $D$ 是好的，当且仅当 $D_{1,1} \times D_{2,2} = D_{1,2} \times D_{2,1}$。其中 $D_{i,j}$ 表示矩阵 $D$ 的第 $i$ 行第 $j$ 列的元素。

小 A 想知道 $A$ 中有多少个好的子矩阵。

输入格式

第一行，两个正整数 $n, m$。

接下来 $n$ 行，每行 $m$ 个整数 $A_{i,1}, A_{i,2}, \ldots, A_{i,m}$。

输出格式

一行，一个整数，表示 $A$ 中好的子矩阵的数量。

输入输出样例 #1

输入 #1

3 4
1 2 1 0
2 4 2 1
0 3 3 0

输出 #1

2

说明/提示

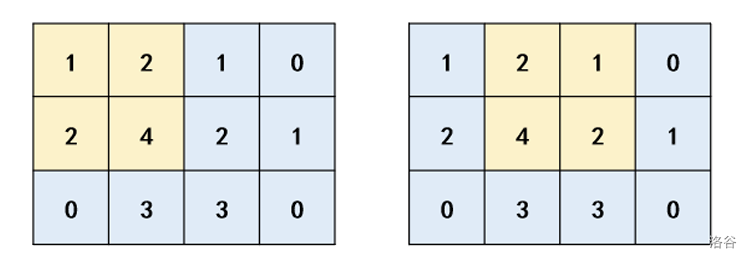
样例解释

样例中好的子矩阵如下：

数据范围

对于所有测试点，保证 $1\leq n\leq 500$，$1\leq m\leq 500$，$-100\leq A_{i,j}\leq 100$

---

题目分析

本题的核心是在一个$n \times m$的矩阵中，找出所有满足条件的$2 \times 2$子矩阵。

1. 数据结构设计

• 使用二维数组num_ary[505][505]存储输入矩阵
• 数组大小设置为505是为了满足题目要求的最大范围($n,m \leq 500$)

2. 核心算法思路

• 遍历所有可能的2×2子矩阵左上角位置
• 行遍历范围：[0, n-2]，确保有足够空间容纳2×2矩阵
• 列遍历范围：[0, m-2]，同理
• 判断：
  • 主对角线：num_ary[i][j] 和 num_ary[i+1][j+1]
  • 副对角线：num_ary[i][j+1] 和 num_ary[i+1][j]
  • 满足条件：num_ary[i][j] * num_ary[i+1][j+1] == num_ary[i][j+1] * num_ary[i+1][j]

3. 算法复杂度分析

1. 时间复杂度
   • 遍历所有可能的 $2 \times 2$ 子矩阵左上角：$O((n-1) \times (m-1))$
   • 每个位置的判断操作：$O(1)$
   • 总体时间复杂度：$O(n \times m)$
2. 空间复杂度
   • 存储输入矩阵：$O(n \times m)$
   • 其他变量：$O(1)$
   • 总体空间复杂度：$O(n \times m)$

---

示例代码

#include <iostream>

// 定义二维数组存储矩阵元素，最大支持500x500的矩阵
int num_ary[505][505];

int main() {
    // 定义矩阵的行数n和列数m
    int n, m;
    // 读入矩阵的行数和列数
    std::cin >> n >> m;

    // 读入矩阵的所有元素
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            std::cin >> num_ary[i][j];
        }
    }

    // 计数器，用于统计满足条件的2x2子矩阵的个数
    int count = 0;
    
    // 遍历所有可能的2x2子矩阵左上角位置
    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j < m - 1; j++) {
            // 判断当前2x2子矩阵是否满足条件：主对角线元素乘积等于副对角线元素乘积
            if (num_ary[i][j] * num_ary[i+1][j+1] == num_ary[i][j+1] * num_ary[i+1][j]) {
                count++;
            }
        }
    }

    // 输出结果
    std::cout << count;
    return 0;
}

---

所有代码已上传至Github：https://github.com/lihongzheshuai/yummy-code

GESP 学习专题站：GESP WIKI

“luogu-”系列题目可在洛谷题库进行在线评测。

“bcqm-”系列题目可在编程启蒙题库进行在线评测。

欢迎加入：Java、C++、Python技术交流QQ群(982860385)，大佬免费带队，有问必答

欢迎加入：C++ GESP/CSP认证学习QQ频道，考试资源总结汇总

欢迎加入：C++ GESP/CSP学习交流QQ群(688906745)，考试认证学员交流，互帮互助

GESP/CSP 认证学习微信公众号